Abstract
The following article demonstrates how Sage/Python can be used to solve, format, and output auto generated code for complex symbolic equations. The auto-generated code can be targeted for languages such as C/C++ or Java. Sage is a computer algebra system (CAS) that uses the Python programming language. By using Python it is easy to write the code and to take full advantage of Python’s text processing capabilities.
Introduction
It is not uncommon for researchers and engineers to need to solve complex symbolic equations in languages like C/C++ and Java. While computer algebra systems (CAS), such as Maple or Mathematica, are designed specifically to handle symbolic math with ease, C style languages are not. A common solution is to first solve the symbolic equations using Maple/Mathematica, then expand out the closed form solution and convert into compilable code.
This process is often easier said than done. What was a nice elegant and compact 3 line equation is expanded out into thousands of lines of code. Hand editing these monstrous equations is not an option. Another issue is that commercial packages such as Maple and Mathematica are both very expensive.
Recently I needed solve an ugly problem in computer vision and having just learned Python, Sage was the obvious choice. Sage is CAS which uses Python as its programming language. Besides being free, Sage is in many ways superior to Maple and Mathematica thanks to Python’s string processing capabilities. The remainder of this article will describe how Sage and Python was used to solve a complex math problem and convert the solution to usable Java code.
The basic for how to use Sage can be found at the following websites:
In this particular application Java code is the final output. However, it is trivial to convert this example to output C/C++ code.
The Math
To demonstrate these techniques a complex real-world problem is used. This problem comes from geometric computer vision and understanding all the math involved is not necessary, but you can find the paper it is based on here [1]. Having an understanding of linear algebra will help you understand all the math terminology. Briefly stated the problem is to solve for a 3×3 Essential matrix given 5 point correspondences. If that means nothing to you, don’t worry.
The first step in solving this problem is computing the null space of a 5 by 9 linear system. The null space is then stored in four column vectors  and
and 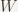 . The final solution is a linear combination of these four vectors:
. The final solution is a linear combination of these four vectors:
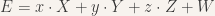
where  is a 3 by 3 Essential matrix being computed,
is a 3 by 3 Essential matrix being computed, 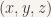 are the scalar variables being solved for. Note that the column vectors are converted into a matrix as needed. Next a system, A, with 10 equations and 20 unknowns is constructed by apply the following constrains on E:
are the scalar variables being solved for. Note that the column vectors are converted into a matrix as needed. Next a system, A, with 10 equations and 20 unknowns is constructed by apply the following constrains on E:
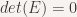
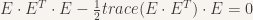
Again if you don’t understand why we are doing the math, don’t panic. Just know that there are some ugly complex equations which need to be solved for in Java. In summary we need to do the following:
- In Java compute the null space and extract out X,Y,Z,W (Not shown)
- In Sage construct a system of equation for the above constraints
- In Sage separate out the known and unknown portions of those equations and output Java code
- In Java solve for unknowns (Not shown)
This is actually only 2/3 of the solution. Since the focus of this article is on the process and not about the details of this particular problem we will skip the rest.
Solving with Sage
All code examples below are written in Python and need to be run inside of Sage’s interactive shell. Do not try to to run the scripts from Python directly, use Sage. All python files need the following imports:
from sage.all import *
from numpy.core.fromnumeric import var |
from sage.all import *
from numpy.core.fromnumeric import var
The first step in solving this problem is creating several 3×3 symbolic matrices. Each element in the matrix is unique. I couldn’t find a function built into Sage, so I wrote my own:
def symMatrix( numRows , numCols , letter ):
A = matrix(SR,numRows,numCols)
for i in range(0,numRows):
for j in range(0,numCols):
A[i,j] = var('%s%d%d' % (letter,i,j) )
return A |
def symMatrix( numRows , numCols , letter ):
A = matrix(SR,numRows,numCols)
for i in range(0,numRows):
for j in range(0,numCols):
A[i,j] = var('%s%d%d' % (letter,i,j) )
return A
The ‘var’ function is used by Sage to define symbolic variables. Inside of the Sage interactive shell you can do the following:
sage: A = symMatrix(3,3,'a')
sage: A
[a00 a01 a02]
[a10 a11 a12]
[a20 a21 a22] |
sage: A = symMatrix(3,3,'a')
sage: A
[a00 a01 a02]
[a10 a11 a12]
[a20 a21 a22]
Now that you can create a symbolic matrix you can solve rest of the problem as follows:
x,y,z = var('x','y','z')
X = symMatrix( 3, 3 , 'X')
Y = symMatrix( 3, 3 , 'Y')
Z = symMatrix( 3, 3 , 'Z')
W = symMatrix( 3, 3 , 'W')
E = x*X + y*Y + z*Z + 1*W
EE = E*E.T
eq1=det(E)
eq2=EE*E-0.5*EE.trace()*E
eqs = (eq1,eq2[0,0],eq2[0,1],eq2[0,2],eq2[1,0],eq2[1,1],eq2[1,2],eq2[2,0],eq2[2,1],eq2[2,2])
keysA = ('x^3','y^3','x^2*y','x*y^2','x^2*z','x^2','y^2*z','y^2','x*y*z','x*y')
keysB = ('x*z^2','x*z','x','y*z^2','y*z','y','z^3','z^2','z','')
# print out machine code for the linear system
printData('A',eqs,keysA)
printData('B',eqs,keysB) |
x,y,z = var('x','y','z')
X = symMatrix( 3, 3 , 'X')
Y = symMatrix( 3, 3 , 'Y')
Z = symMatrix( 3, 3 , 'Z')
W = symMatrix( 3, 3 , 'W')
E = x*X + y*Y + z*Z + 1*W
EE = E*E.T
eq1=det(E)
eq2=EE*E-0.5*EE.trace()*E
eqs = (eq1,eq2[0,0],eq2[0,1],eq2[0,2],eq2[1,0],eq2[1,1],eq2[1,2],eq2[2,0],eq2[2,1],eq2[2,2])
keysA = ('x^3','y^3','x^2*y','x*y^2','x^2*z','x^2','y^2*z','y^2','x*y*z','x*y')
keysB = ('x*z^2','x*z','x','y*z^2','y*z','y','z^3','z^2','z','')
# print out machine code for the linear system
printData('A',eqs,keysA)
printData('B',eqs,keysB)
The functions det and trace compute the determinant and trace of a matrix respectively, A.T is the transpose of A. Most of that is straight forward algebra, but what about that last bit? Well the printData() function massages those equations to produce usable Java output, which is the subject of the next section.
Generating Code
What the Java code is going to do is solve a linear system. To do that the equations above need to reformatted and converted into matrix format. The variable eqs in the above python code contains equations which have a similar appearance to the equation below on the left, but they need to be expanded out so that they look like the equation on the right.
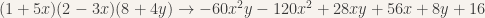
After the equations have been expanded, the knowns and unknowns are separated and put into matrix format. Consider the system of equations below:

After it has been converted into matrix format it will look like:
![A=\left[ \begin{array}{ccc} 1 & 2 & 3 \\ 5 & 6 & 7 \\ 9 & 10 & 11 \\ \end{array} \right] \;\; B=\left[ \begin{array}{c} 4 \\ 8 \\ 12 \\ \end{array} \right] A=\left[ \begin{array}{ccc} 1 & 2 & 3 \\ 5 & 6 & 7 \\ 9 & 10 & 11 \\ \end{array} \right] \;\; B=\left[ \begin{array}{c} 4 \\ 8 \\ 12 \\ \end{array} \right]](https://s0.wp.com/latex.php?latex=A%3D%5Cleft%5B++%5Cbegin%7Barray%7D%7Bccc%7D++1+%26+2+%26+3+%5C%5C++5+%26+6+%26+7+%5C%5C++9+%26+10+%26+11+%5C%5C++%5Cend%7Barray%7D++%5Cright%5D++%5C%3B%5C%3B++B%3D%5Cleft%5B++%5Cbegin%7Barray%7D%7Bc%7D++4+%5C%5C++8+%5C%5C++12+%5C%5C++%5Cend%7Barray%7D++%5Cright%5D&bg=f7f3ee&fg=333333&s=0)
At this point the unknowns can be solved for using standard linear algebra tools, e.g. Ax=B.
Part of this process is shown below. First eq1 is expanded out and then the coefficients of 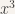 are extracted.
are extracted.
sage: len(str(eq1))
465
sage: len(str(eq1.expand()))
7065
sage: extractVarEq(eq1.expand(),'x^3')
'X00*X11*X22 - X00*X12*X21 - X01*X10*X22 + X01*X12*X20 + X02*X10*X21 - X02*X11*X20' |
sage: len(str(eq1))
465
sage: len(str(eq1.expand()))
7065
sage: extractVarEq(eq1.expand(),'x^3')
'X00*X11*X22 - X00*X12*X21 - X01*X10*X22 + X01*X12*X20 + X02*X10*X21 - X02*X11*X20'
The first two statements are just there to show you how long and ugly these equations are. Below is the python code for extractVarEq:
def extractVarEq( expression , key ):
chars = set('xyz')
# expand out and convert into a string
expression = str(expression.expand())
# Make sure negative symbols are not stripped and split into multiplicative blocks
s = expression.replace('- ','-').split(' ')
# Find blocks multiplied by the key and remove the key from the string
if len(key) == 0:
var = [w for w in s if len(w) != 1 and not any( c in chars for c in w )]
else:
var = [w[:-(1+len(key))] for w in s if (w.endswith(key) and not any(c in chars for c in w[:-len(key)])) ]
# Expand out power
var = [expandPower(w) for w in var]
# construct a string which can be compiled
ret = var[0]
for w in var[1:]:
if w[0] == '-':
ret += ' - '+w[1:]
else:
ret += ' + '+w
return ret |
def extractVarEq( expression , key ):
chars = set('xyz')
# expand out and convert into a string
expression = str(expression.expand())
# Make sure negative symbols are not stripped and split into multiplicative blocks
s = expression.replace('- ','-').split(' ')
# Find blocks multiplied by the key and remove the key from the string
if len(key) == 0:
var = [w for w in s if len(w) != 1 and not any( c in chars for c in w )]
else:
var = [w[:-(1+len(key))] for w in s if (w.endswith(key) and not any(c in chars for c in w[:-len(key)])) ]
# Expand out power
var = [expandPower(w) for w in var]
# construct a string which can be compiled
ret = var[0]
for w in var[1:]:
if w[0] == '-':
ret += ' - '+w[1:]
else:
ret += ' + '+w
return ret
The function expandPower(w) converts statements like a^3 into a*a*a which can be parsed by Java. After processing all 10 equations most of the hard work is done, Addition processing is done to simplify the equations, but the code is a bit convoluted and isn’t discussed here. The final output it sent into a text file and then pasted into a Java application.
Want to see what the final output looks like? Well here is a small sniplet:
A.data[0] = X20*( X01*X12 - X02*X11 ) + X10*( -X01*X22 + X02*X21 ) + X00*( X11*X22 - X12*X21 );
A.data[1] = Y02*( Y10*Y21 - Y11*Y20 ) + Y00*( Y11*Y22 - Y12*Y21 ) + Y01*( -Y10*Y22 + Y12*Y20 );
A.data[2] = X22*( X00*Y11 - X01*Y10 - X10*Y01 + X11*Y00 ) + X20*( X01*Y12 - X02*Y11 - X11*Y02 + X12*Y01 ) + X21*( -X00*Y12 + X02*Y10 + X10*Y02 - X12*Y00 ) + X01*( -X10*Y22 + X12*Y20 ) + Y21*( -X00*X12 + X02*X10 ) + X11*( X00*Y22 - X02*Y20 ); |
A.data[0] = X20*( X01*X12 - X02*X11 ) + X10*( -X01*X22 + X02*X21 ) + X00*( X11*X22 - X12*X21 );
A.data[1] = Y02*( Y10*Y21 - Y11*Y20 ) + Y00*( Y11*Y22 - Y12*Y21 ) + Y01*( -Y10*Y22 + Y12*Y20 );
A.data[2] = X22*( X00*Y11 - X01*Y10 - X10*Y01 + X11*Y00 ) + X20*( X01*Y12 - X02*Y11 - X11*Y02 + X12*Y01 ) + X21*( -X00*Y12 + X02*Y10 + X10*Y02 - X12*Y00 ) + X01*( -X10*Y22 + X12*Y20 ) + Y21*( -X00*X12 + X02*X10 ) + X11*( X00*Y22 - X02*Y20 );
The full source code can be downloaded from:
[1] David Nister “An Efficient Solution to the Five-Point Relative Pose Problem” Pattern Analysis and Machine Intelligence, 2004
